社会design论期末复习

モデルは⽤途によって,様々な粒度(こまかさ)があり得るが,⼤別すると,マクロ的なモデル(粗い・粗粒度のモデル)か,ミクロ的なモデル(細かい・細粒度のモデル)か
システムダイナミクス(SD)とは 1950年代後半にマサチューセッツ⼯科⼤学のフォレスター(J.W.Forrester)が発想• システムを構成する要素の経時的な変化が他の要素にどのような変化をもたらすか,またその時に,システム全体ではどのような変化が⽣じるかをマクロな視点で(すなわち,俯瞰的に)捉えるシミュレーションの技法
SDはシステム内のそれぞれの要素の状態を時間変化に基づく⽅程式で表現し,システム全体の動的変化をシミュレートする
因果ループ図: 対象とするシステムに内在する要素の相互関係を図式化したもの
- "-"の数が奇数なら全体として負のフィードバックループ,偶数なら全体として正のフィードバックループとなる
SDによるシミュレーションはシステム全体の状態変化をマクロな視点から⾒るには適した⼿法
- 時系列に従った予測(シミュレーション)ではあるが,現状のパラメータ値のもとで将来を予測している
- いくつかのパラメータのセット(シナリオ)を⽤いてシミュレーションを⾏い,個々の条件下でどのような変化が⽣じるかを提⽰するには役⽴つ⼿法
エージェントは⾃ら判断し⾏動する主体
なぜエージェントが必要か? • ソフトウェア危機
- ソフトウェアライフサイクルの短期化 Ø ⼀からソフトウェアを作っていられない (=ソフトウェアの再利⽤・部分開発)
- オープンシステム化 Ø いろいろなものを組み合わせる技術
- ⼤規模・分散システム化 Ø 複数個のシステムを連携させ1つのサービスを構築する
- インターネットの発展 Ø いつでも,誰にでも使え,信頼できるシステムが求めら れる Øオブジェクト指向
ソフトウェアが「⾃律性」を持つ必要がある • オブジェクトは基本的に「受動的」 • エージェントはオブジェクトに「能動性」や「⾃律 性」を付加したもの
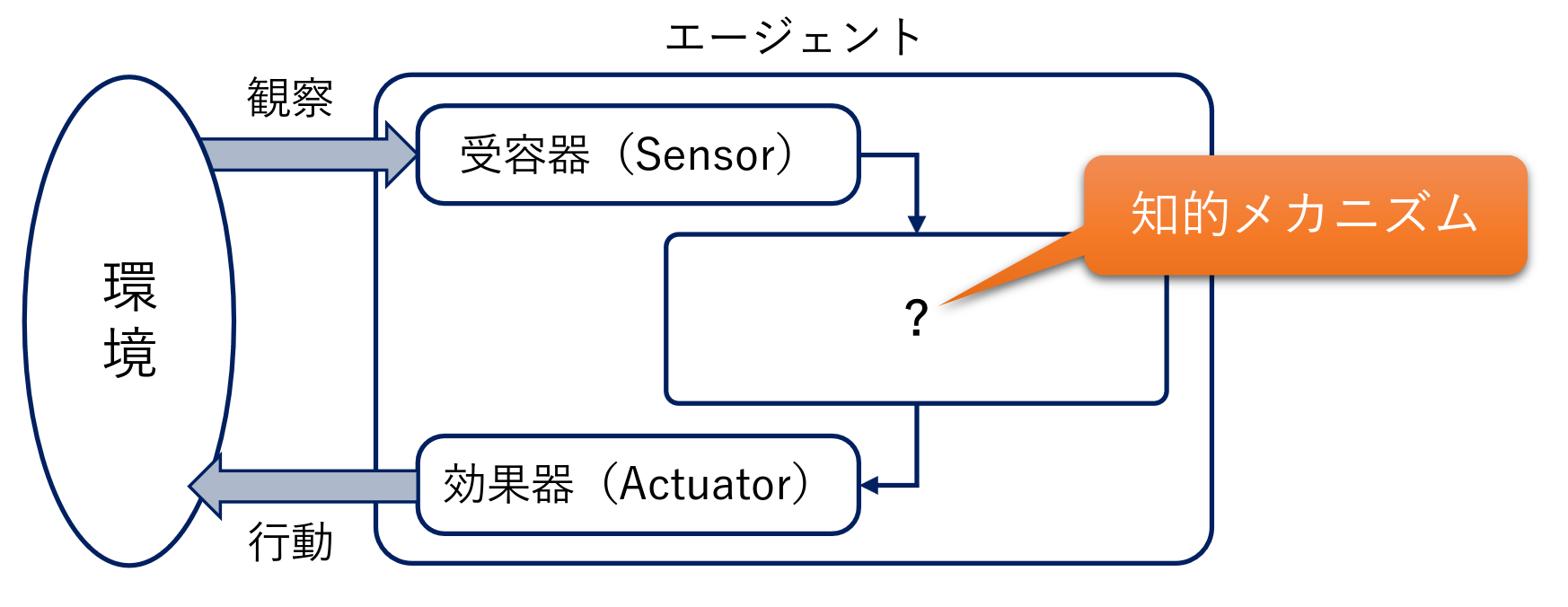
エージェントは環境をセンサ(S)を通じて知覚し, 環境にアクチュエータ(A)を通じて作⽤する
性能指標(performance measure) • エージェントがどの程度成功したかを評価する基準
知的メカニズムのレベルに基づき,(1) 反射エージェント, (2) 内部状態に基づくエージェント,(3) ⽬的に基づく エージェント,(4) 効⽤に基づくエージェントに分類
反射エージェント 「条件-⾏動ルール」を持ち,知覚した環境情報から⾏動を導く • 複数のルールが利⽤可能な場合は,1つのルールを選択 ü 環境の状態のみで適切な⾏動決定ができる場合に有効
内部状態に基づくエージェント 内部状態とセンサによる知覚情報を組み合わせた環境 条件から⾏動を選択する ü 環境の状態と内部状態のみで適切な⾏動を決定できる場合に 有効
⽬的に基づくエージェント 内部状態とセンサによる知覚情報を組み合わせた環境 条件の下で適⽤可能な各ルール実⾏時の次状態を推定 • 推定された次状態に基づき,⼀つのルールを選択・実⾏する • ルールの選択戦略は様々(e.g., ゴール最近傍,期待値ベースなど) ü ゴール達成が要求される場合に有効
効⽤に基づくエージェント • ゴールに基づく「救急⾞」が病院に辿り着く事は最低 限の要求であり,いかに早く,安全に,かつ低いコス トで到着するかという複数の⽬的は満たせない • スピードと安全性といった相容れない⽬的の対処は困難 Ø 複数の⽬的を「効⽤関数」としてゴールに換えて組み⼊れる 環境条件の下で適⽤可能な各ルール実⾏時の次状態を 推定,までは⽬的に基づくエージェントと同じだが... • 各々の次状態の効⽤(好ましさ)を計算し,最も効⽤の⾼い ルールを選択・実⾏する ü 様々な状況に対処しやすく,有効なアーキテクチャ
学習エージェント • 熟考的なエージェントを以下の機構で拡張する • ルールの価値の修正 • 環境が複雑になると次状態の効⽤の正確な計算は困難になる.そこ で,結果に基づきルールの価値を修正する機構を追加する • ルールの⽣成と削除 • 所与の「条件-⾏動ルール」だけで全ての状況への対応は困難であ るため,必要に応じて新たなルールを作成する機構を追加する • 無限にルールを⽣成・保持するのは困難・⾮効率であるため,適切 な削除機構も追加する
マルチエージェントシステム=⼈間社会に⾒ら れる組織的な問題解決や調整を⾏う⼈⼯システ ムの構築 • マルチエージェントシステムでは,個々のエー ジェントの構成よりも,エージェント間のイン タラクションの仕組みと構築に⼒点が置かれる
インタラクションの2つの形態 • 協⼒:エージェントの持つ⽬標が共通 • 競合:エージェントの持つ⽬標が対⽴
協⼒型マルチエージェントシステム =共通の⽬標に向けて複数のエージェントが協調 • タスク共有と結果共有 • タスク共有 • タスクの各要素がエージェントに分散 • 問題解決に要する負荷を予め複数のエージェントに分割して割 り当てる協調の形式 • 各エージェントが独⽴にタスクを解けることを前提とする • 結果共有 • 情報(知識源)が分散 • 複数のエージェントが独⽴の⾒地から問題の部分的な解を持ち 寄る協調の形式
契約ネットプロトコル(Contract Net Protocol)は, 問題を多数のエージェントのネゴシエーションを通じ て分割し,各エージェントにタスクを割り当てる • ネゴシエーション(negotiation)は,複数のエージェントが 情報交換を通じて合意を得るプロセス • 契約の提案側エージェントをマネージャ(manager), 請負側エージェントは契約者(contractor)と呼ぶ
まずマネージャがタスク告⽰を⾏う • 契約者にとってみれば「タスク告⽰」(Task Announcement) を⾏うマネージャはネットワーク内に多数存在す
従って,契約者は多数の「タスク告⽰」から「⼊札」 (bid)するマネージャを,契約者独⾃の価値基準で選択 する
よって,マネージャは多数の「⼊札」から,「落札」 (award)する契約者を,マネージャ独⾃の価値基準で 選択する • マネージャと契約者が「⼊札」「落札」に際して独⽴ の価値基準を持つ.このしくみは相互選択(mutual selection)と呼ばれる
ゲーム理論
- プレイヤ
- ⾏動
- 利得: プレイヤの⾏動の組み合わせに対して定義される数値として表す
利得⾏列(利得表)
プレイヤは合理的(rational)であると仮定するので
- ⾃分の効⽤最⼤化のために最⼤限の努⼒をし、他⼈の効⽤には無関⼼
⽀配戦略(dominant strategy): 相⼿がどの⾏動を選ぼうが,他の戦略よりも得られる効⽤が⾼い(か少なくとも同じ) 戦略
⽀配戦略均衡: 両⽅のプレイヤが⽀配戦略を持つ時,結果は⽀配戦略均衡
反復⽀配戦略均衡: 「相⼿の得は⾃分の損」となるゼロサムゲームの⼀種
- ⽀配されている戦略を交互に取り除き,最後に残った戦略の組み合わせを反復⽀配戦略均衡という
ミニマックス戦略:相⼿の⾏動により⽣じ得る最悪の場合を想定し、その最悪の場合に⾃分にとって最良の⾏動を採る戦略
鞍点 • 両プレイヤの⾏動の交点は、横から⾒ると極⼩の点となり、縦から⾒ると極⼤の点となる • 利得表を3次元空間上にプロットすると⾺の鞍のような形状が描かれる
合理的なプレイヤによるゲームでは、(存在すれば)⽀配戦略均衡に⾄る事が予想される
「社会的に望ましい状態」=パレート効率な状態
全ての⼈が合意できる,より良い状態がない =誰かの効⽤を犠牲にせず他のプレイヤの効⽤を向上できない • ゼロサムゲームではどの解でもパレート効率的。
合理的で賢いプレイヤなのに,社会的に望ましいパレート効率的な状態にたどりつけない: 囚⼈のジレンマ
戦略(⾏動)の組(s, t)が、互いに相⼿の⾏動に対する最適な反応となっている時、この戦略の組はナッシュ均衡になっている • ⽀配戦略均衡ならば、それは必ずナッシュ均衡(ただし、逆は⾔えない) • ゼロサムゲームの鞍点はナッシュ均衡 • ナッシュ均衡が唯⼀のものであれば、合理的プレイヤによるゲームはナッシュ均衡に落ち着く • 他の状態は不安定
グラフ理論 -> 複雑ネットワーク
オブジェクトをノードまたは頂点、つながりをエッジとし、それらが組み合わさったものがグラフ • N: ノード (node)、または頂点 (vertex) からなる集合 • E: 点をつなぐ辺 (edge) からなる集合 • G: N と E の集合
N = {n1 , n2 , n3 , n4 }
𝐸 = {𝑒1=(n1 ,n3 ), 𝑒2 ={n2 ,n3 },
𝑒3 ={n3 ,n4 }, 𝑒4 ={n2 ,n4 }}
𝐺 = {N, 𝐸}次数(degree) • 頂点n𝑖から出ている辺の数 • deg(n𝑖)
「任意の⼆つの頂点が全て隣接している」事を特別な状態とみなし、完全グラフ(クリーク)と呼ぶ
ランダムグラフ(ネットワーク) • n個のノードがある時,2頂点間に確率pでリンクをつなぐ
pが⼤きくなるにつれていくつかの塊ができ,徐々に連結する • p≧logN/Nでネットワーク全体が連結する
分布:pN(N-1)/2
現実世界のネットワークのスモールワールド性 ネットワークの規模は⼤きいにも関わらず、任意の2つのノードがわずかな数のノードを介するだけで接続される性質
現実世界のネットワークのクラスタ性 ネットワーク中にノード同⼠が互いに密に結びつき合った部分(サブグラフ)が存在するという性質
現実世界のネットワークのスケールフリー性 ⼀部のノードが多数のノードと繋がっているのに対し、⼤多数のノードはわずかなノードとしか繋がっていない性質 • ハブの存在
スケールフリーネットワーク • エッジの数がベキ法則に従って分布(べき乗分布) 正規分布とは異なり、中央値から極端に⼤きく外れたデータが無視できない割合で存在する、裾野の⻑い分布
ネットワークの特徴量 (1) 次数分布 (2) 平均経路⻑: ネットワークのおおよその⼤きさを表現可能 (3) クラスタ係数 (4) 次数相関 (5) 中⼼性 • 次数 • 近接中⼼性 • 媒介中⼼性 • ページランク
次数分布 • 各ノード(頂点)の次数がいくつあるか,その分布
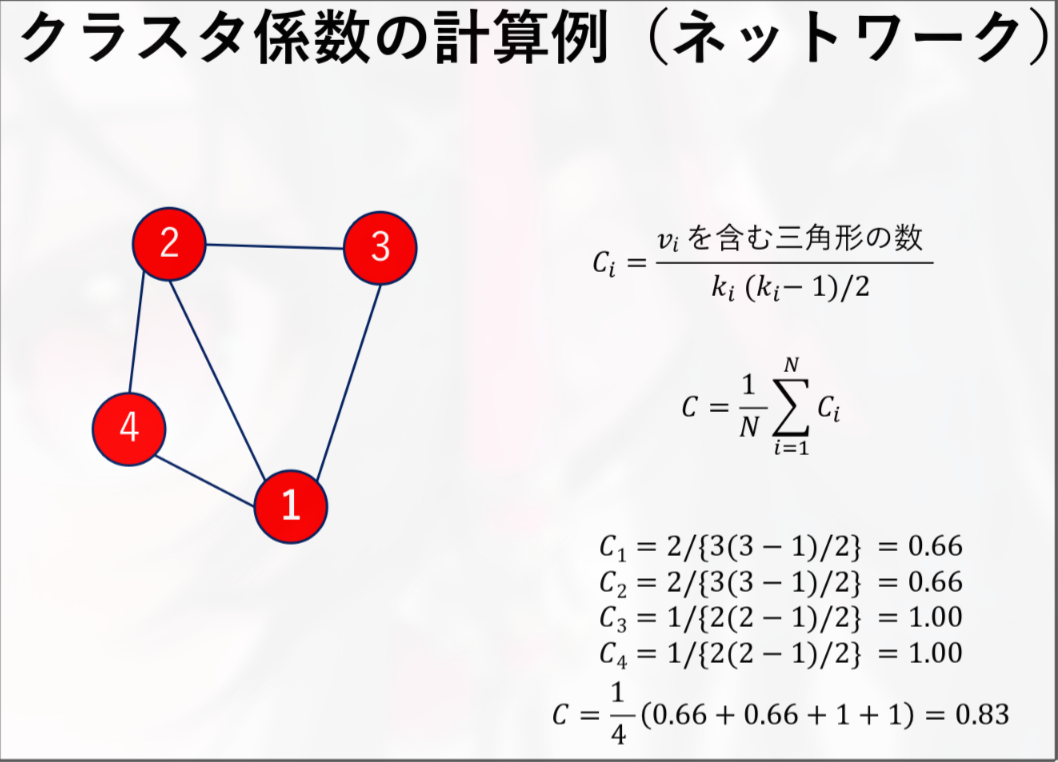
クラスタ係数
• クラスタ:ネットワーク中で密に繋がっている部分(例:三⾓ネットワーク)
次数相関(同類選択性)接続ノード間の次数の相関係数 • 正の数 • ⾼次数ノードは,⾼次数ノードと隣接しやすい • 負の数 • ⾼次数ノードは,低次数ノードと隣接しやすい
中⼼性 • ノードの特徴を調べる特徴量 • 次数中⼼性: 次数そのもの • 近接中⼼性: すべてのノードからの距離
- 各頂点から他の頂点までの距離の総和が⼩さいほど中⼼,とみなされる
- (N-1)/Sum(every d) • 媒介中⼼性: 他のノードにたどり着くために当該ノードを通らなければいけない割合
- TODO:
ページランク: TODO
模拟的验证与验证(Verification & Validation):
- Verification:模型是否按预期工作(类似于软件开发中的调试)。
- Validation:是否能够适当地再现现实世界(的目标)(衡量现实与计算结果的差异程度)。
シミュレーションの分類 • 静的モデル: 時系列に沿った進化・発展を考慮せずに,定常状態での対象の性質を表現・分析するモデル e.g. 損益分岐点分析,線形計画法,クラス図 • 動的モデル: 時間の経過と共に変化する対象の推移を観察するモデル • 連続変化モデル:時間の経過と共に連続的に変化する事象を表現 e.g., 微分⽅程式など • 離散変化モデル:離散的な時間間隔で変化する事象を表現 e.g., 在庫・待ち⾏列問題(在庫の到着や引き取り,客の到来をきっかけに変化する)
シミュレーションの技法 • モンテカルロ法: 为处理包含不确定因素的现象,使用随机数的模拟技法的总称。 • 待ち⾏列モデル • セルオートマン • マルチエージェントシミュレーション
待ち⾏列モデルの種類 • 定期到着,定期サービス: • ランダム到着,定期サービス: • 定期到着,ランダムサービス: • ランダム到着,ランダムサービス:
排队理论 肯德尔符号:A/B/C/K/N/Z 用斜杠分隔来描述排队的六个元素 A:到达过程 B:服务时间 C:窗口数量 K:系统容量 N:客户最大数量 Z:服务规则
排队模型 M/M/c 客户的到达遵循泊松过程(指数分布),服务时间也服从指数分布,且有c个服务窗口的排队模型。 M/M/c是最基础的排队模型之一,可以用来解析性(数学性)地解决可能出现的排队问题。
デザイン⽅法論