functional basics

参照透明性（Referential Transparency, RT）是一个非常重要的概念。理解它可以帮助你更好地编写和理解函数式代码。下面是关于参照透明性的一些关键点：

定义： 参照透明性是指在程序中，如果一个表达式可以被它的值替换，而不会改变程序的行为，那么这个表达式就是参照透明的。换句话说，给定相同的输入，一个表达式总是产生相同的输出，而不会产生任何副作用。

无副作用： 在满足参照透明性的系统中，函数是没有副作用的。这意味着函数不会修改外部状态，也不依赖于外部状态。它们只依赖于传入的参数，并且总是返回相同的结果。

可推导性和可理解性： 由于参照透明性，程序的行为更容易推导和理解。你可以通过查看函数的定义和它的输入来理解函数的行为，而不需要考虑外部的环境或状态。

等式推理： 参照透明性使得程序员可以安全地进行等式推理，这是一种通过将表达式替换为等价的表达式来推导程序行为的方法。这对于理解和重构代码非常有用。

优化： 编译器也可以利用参照透明性来进行优化，例如通过消除重复的函数调用，或者通过重新排序不依赖于彼此的函数调用来提高性能。

纯函数： 在函数式编程中，参照透明性通常与纯函数（Pure Functions）联系在一起。纯函数是指给定相同输入总是产生相同输出，并且没有副作用的函数。

functional programming: Programming without assignment statements

If you want to get rid of assignment statements, you have to use recursion. Recursion allows you to replace the assignment of local variables with the initialization of function arguments

tail call optimization (TCO) and all functional languages make use of it.1

The Java virtual machine (JVM) complicates TCO a bit. C, of course, does not do TCO and so all my recursive examples in C will grow the stack.

just remember when you use recursion to eliminate assignment statements, you are not necessarily wasting lots of space on the stack. The language you are using is almost certainly using TCO

sequential or temporal coupling—a coupling in time; and it is something you are probably quite familiar with. Open must be called before close. New must be called before delete. Malloc must be called before free. The list of pairs2 like this is endless

When two or more threads are competing for the processor, keeping the temporal couplings in the correct order becomes a much more significant challenge.

temporal coupling and race conditions: order problem

State system(State s) {
  return isFinal(s) ? s : system(s);
}
 
// a “functional” program that responds quite nicely to input events
 
State system(State state, Event event) {
  return done(state) ? state : system(state, getEvent());
}

getEvent() is not purely functional. but functional programming is about the style.

#include <stdio.h>
 
typedef enum {locked, unlocked, done} State;
typedef enum {coin, pass, quit} Event;
 
void lock() {
  printf("Locking.\n");
}
 
void unlock() {
  printf("Unlocking.\n");
}
 
void thankyou() {
  printf("Thanking.\n");
}
 
void alarm() {
  printf("Alarming.\n");
}
 
Event getEvent() {
  while (1) {
    int c = getchar();
    switch (c) {
      case 'c': return coin;
      case 'p': return pass;
      case 'q': return quit;
    }
  }
}
 
State turnstileFSM(State s, Event e) {
  switch (s) {
    case locked:
    switch (e) {
      case coin:
      unlock();
      return unlocked;
 
      case pass:
      alarm();
      return locked;
 
      case quit:
      return done;
    }
 
    case unlocked:
    switch (e) {
      case coin:
      thankyou();
      return unlocked;
 
      case pass:
      lock();
      return locked;
 
      case quit:
      return done;
    }
    case done:
    return done;
  }
}
 
State turnstileSystem(State s) {
  return (s==done)? 0
                  : turnstileSystem(
                      turnstileFSM(s, getEvent()));
}
 
int main(int ac, char** av) {
  turnstileSystem(locked);
  return 0;
}

Persistent Data

The Sieve of Eratosthenes: “埃拉托色尼筛法”或“埃拉托斯特尼筛法”。一种用来寻找一定范围内所有素数的古老算法，由古希腊数学家埃拉托斯特尼（Eratosthenes）在公元前3世纪发明。通过这种方法，你可以高效地找到小于或等于某个给定数的所有素数。该算法的基本思想是从2开始，将所有2的倍数标记为非素数，然后找到下一个未被标记的数，并将其所有的倍数标记为非素数，如此循环，直到所有的数都被检查过为止。

package sieve;
 
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
 
public class Sieve {
  static List<Integer> primesUpTo(int upTo) {
    return getPrimes(
      computeSieve(
        makeSieve(Math.max(upTo, 1)),
        0),
      new ArrayList<>(), 0);
  }
 
  private static boolean[] makeSieve(int upTo) {
    boolean[] sieve = new boolean[upTo+1];
    Arrays.fill(sieve, false);
    sieve[0] = sieve[1] = true;
    return sieve;
  }
 
  private static boolean[] computeSieve(boolean[] sieve, int n) {
    if (n>=sieve.length)
      return sieve;
    else if (!sieve[n])
      return computeSieve(markMultiples(sieve, n, 2), n+1);
    else return computeSieve(sieve, n+1);
  }
 
  private static boolean[] markMultiples(boolean[] sieve,
                                         int prime,
                                         int m) {
    int multiple = prime * m;
    if (multiple>=sieve.length)
      return sieve;
    else {
      var markedSieve = Arrays.copyOf(sieve, sieve.length);
      markedSieve[multiple] = true;
      return markMultiples(markedSieve, prime, m+1);
    }
  }
 
  public static List<Integer> getPrimes(boolean[] sieve,
                                        List<Integer> primes,
                                        int n) {
    if (n>=sieve.length)
      return primes;
    else if (!sieve[n]) {
      var newPrimes = new ArrayList<>(primes);
      newPrimes.add(n);
      return getPrimes(sieve, newPrimes, n+1);
    } else {
      return getPrimes(sieve, primes, n+1);
    }
  }
}

The Church–Turing thesis tells us that Turing machines and lambda calculus are equivalent forms; but that doesn’t mean you can easily translate from one to the other. A functional program is a program that looks like lambda calculus but is implemented in a finite Turing machine. And that implementation requires that we cheat

Church-Turing Thesis： Church-Turing Thesis 是一个基础性的假设，它表明所有“有效计算”都可以通过图灵机（Turing machines）或者λ演算（lambda calculus）来表达。这两种计算模型在能力上是等价的，即它们能够计算相同的问题集合。

Turing Machines 和 Lambda Calculus：

• 图灵机是一种抽象的计算模型，它由一个无限长的纸带、一个读写头和一套控制规则组成。图灵机能够模拟任何算法的逻辑。
• λ演算是一种基于函数抽象和函数应用的计算模型，它通常用于描述和分析函数式编程语言。

函数式程序与实现： 函数式程序通常是以λ演算为基础来设计的，它强调使用函数和避免状态变化。但在实际的计算机系统中，它们是通过图灵机模型（或者说，通过现实中的有限状态机、计算机硬件）来实现的。这里的“有限图灵机”可能是指在现实世界中，资源（如内存）是有限的，与理论中的无限图灵机不同。

The first cheat we saw was TCO. We waved it away with an argument about pragmatics. After all, since we were never going to need all those historical stack frames, why should we keep them? But that’s still a cheat. Under the hood, our implementation was changing the values of existing variables. From the Turing machine’s point of view, all our supposed constants were actually variables.

We could continue to push that cheat upward. This lovely little Sieve algorithm runs entirely in the constructor, so it’s all initialization! And as we learned, initialization is not assignment. So the fact that this program has variables under the hood is no different from TCO. In the end, the result is still functional.

TCO is a practically unavoidable cheat.

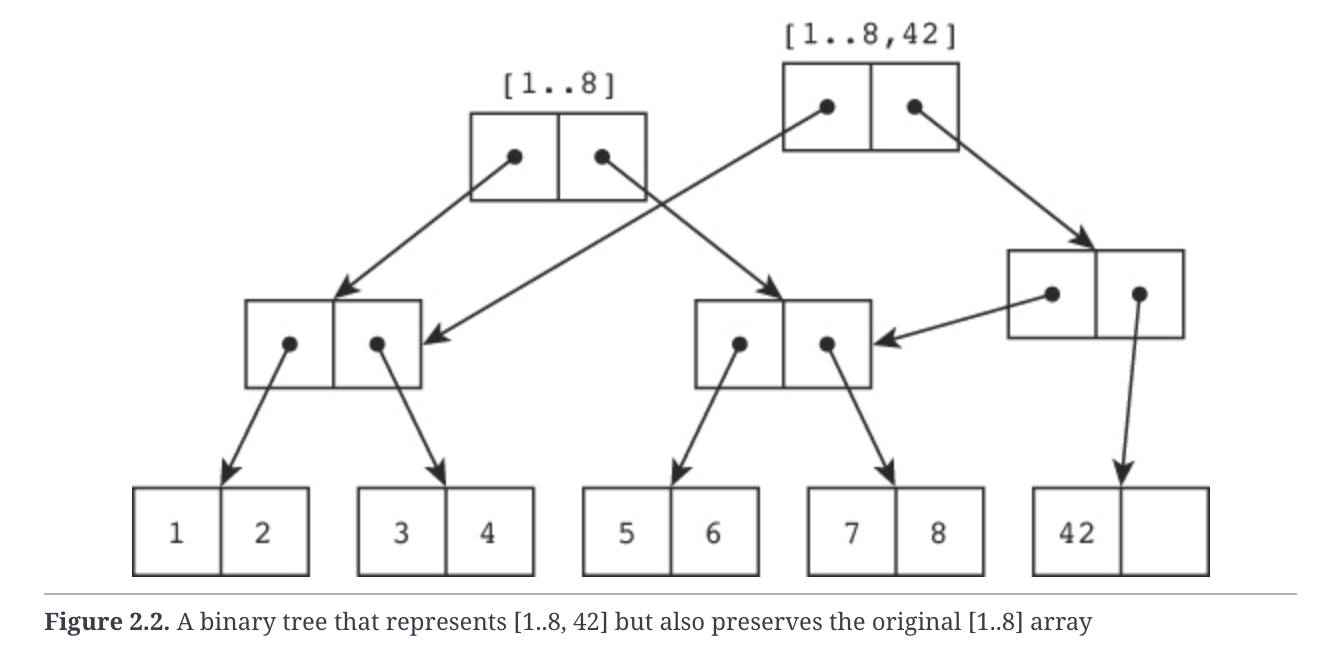
data structures that behave very much like arrays but that also efficiently maintain the history of their past states. These data structures are n-ary trees. The bigger the n, the more efficient they are. But for the sake of simplicity, I will choose an n of 2—binary trees